After starting this Weblog in January 2015 and as a new user of WordPress, I tried to customize the settings that would bring pertinent comments to this blog site and discourage trolling, tangential, self-serving, generalized, content-praising, off-topic messages.
In February, I published two posts, one at the beginning of February, and one on February 19. The first post had a Greek letter in the title. The second post had all English words.
Prior to February 19, what was merely a low single digit daily trickle of comments turned into a deluge starting on February 21. Comments were made not only to my blog posts – one of which was WordPress’ “Hello, World” – but also to my “About …” page and a Sample Page. I thought it amusing that the commentary on these pages praised with the same fervor as my actual blog posts.
From February 21 through February 25, 2015, I received nearly 800 comment |S,p.a,m| messages. I was curious to see if I could analyze these messages further beyond their individual hooks to communicate back.
[1] WHEN: Date and Time
I noticed that they arrived in clumps at differing times each day. So I created an overlapping frequency distribution using 24 hourly intervals and superimposed 4 days, 7 hours of Comment Email notifications based on arrival time (Universal Time) for moderation. It looks like this [Click to remove vaseline and enlarge]:
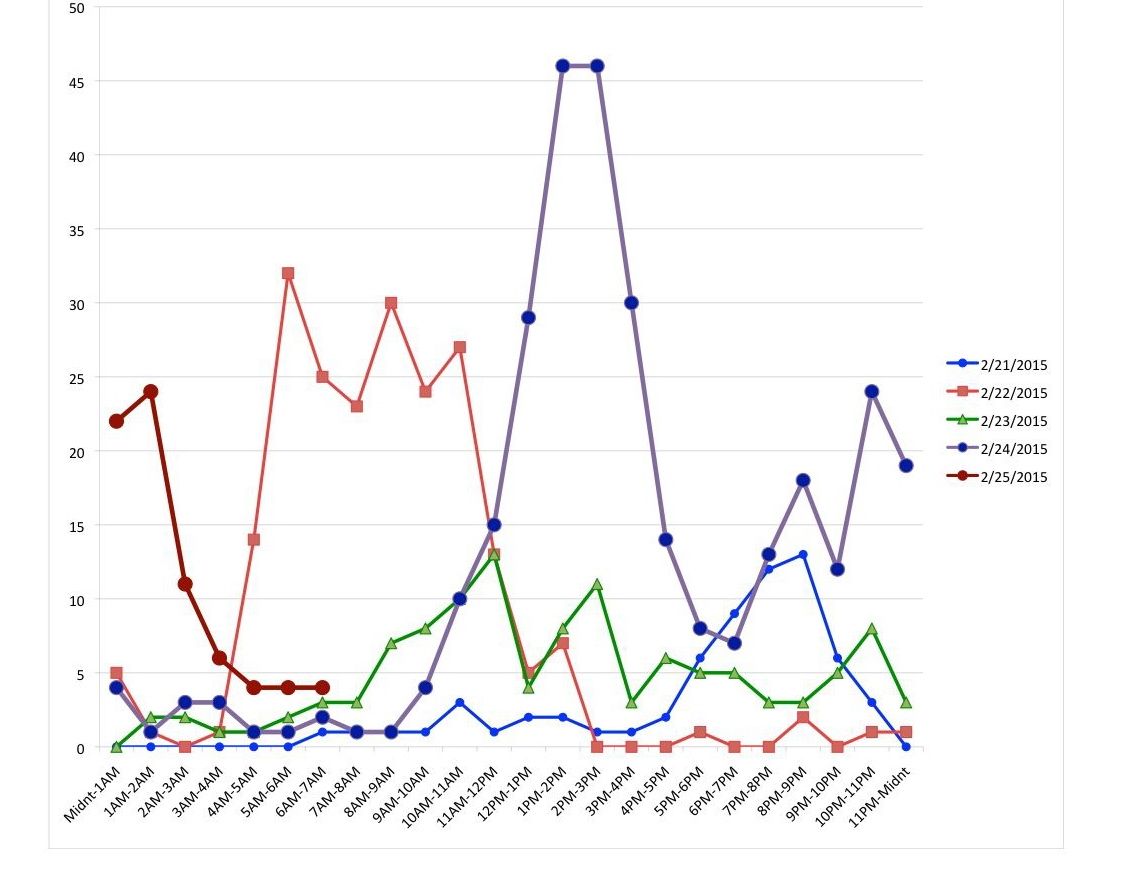
| Characteristic | # Emails | Date | Time Interval(s) |
| Maximum | |||
| 13 | 2-21-2015 | 8-9PM | |
| 32 | 2-22-2015 | 5-6AM | |
| 13 | 2-23-2015 | 11AM-12PM | |
| 46 | 2-24-2015 | 1-2PM, 2-3PM | |
| 24 | 2-25-2015 | 1-2AM | |
| Total Messages | |||
| 65 | 2-21-2015 | 6AM-Midnight | |
| 212 | 2-22-2015 | ||
| 116 | 2-23-2015 | ||
| 312 | 2-24-2015 | ||
| 75 | 2-25-2015 | Midnight-7AM | |
| Peak Arrival(s) | |||
| 46 | 2-21-2015 | 5-10PM | |
| 118 | 2-22-2015 | 4AM-12PM | |
| 61 | 2-23-2015 | 8AM-3PM | |
| 190 | 2-24-2015 | 10AM-5PM | |
| 143 | 2-24-2015 & | 7PM-3AM | |
| 2-25-2015 |
The Peak Arrival duration seemed to be between 7 and 8 hours, once it got started on 2-22-15, with somewhat increasingly higher numbers of Emails showing up. It felt like new UTC time zones were activated over the days. Moscow and the Middle East on 2-22-15, Western Europe on 2-23-15, Iceland, Brazil and into New York on 2-24-15 and Vladivostok on the evening of 2-24-15 and continuing into 2-25-15.
Since I was spending a successively greater amount of my day reading the comments (to make sure a genuine comment wasn’t lurking) and isolating these moderation requests with no expectation that it would taper off soon and with full expectation that my next blog post would produce even greater unwanted feedback. I decided to “pull the plug”.
I updated the comment rules to include all those wishing to comment to register first. This stopped all the comments completely by 7:30AM UT on 2-25-15. It appears that the comments I experienced were programmatically generated, once postings on my blog site was made available to these sources.
I was curious also about who and where these false commentators came from. At first, I thought I could capture salient characteristics of each comment in an Excel Spreadsheet, but it required me to do repeated copy and paste from my Browser to Excel. As the comments mounted, it appeared that I would invest a large amount of time chasing upwards of 780 messages.
So I decided to review the E-mail message stream sent to me that indicated that a comment just arrived and needed approval moderation. Because such a single E-mail message could be associated with more than one comment, there were 605 such E-mail notifications, still making for a fairly large sample.
In order to process the information in a few minutes rather than a few weeks, I decided to use my Unix/Linux skills on MacOSX via the underlying commandline application called terminal.
The Characteristics I sought were:
- [1] Date and Time of arrival of a message
- [2] Page or Post that was targeted
- Author (with IP address)
- [3] Author alone
- [4] Whois IP address information and Corresponding Cities and Countries
- Email addresses that were used
- [5] Email domains on the right side of the @ sign
- [6] URL with a segregation of https and http communication protocols
- [7] Selected Key words or phrase characteristics used in messages
I diligently moved all inbox mail in mail.app sent from WordPress requesting moderation to a mail account |S,p.a,m| folder.
Next, I checked with Google about where the MacOSX mail.app keeps the directory of a mail account’s |S,p.a,m| folder.
Once this was known, I began to write a bash script to extract into separate files the information listed above (as well as produce more analyzed reports).
Here is the bash script:
#! /bin/bash
USAGE="Usage: spamscript.bash"
# Created by Robert 2/25/2015 to Analyze Blog Spam
#
DIR=~/library/Mail/IMAP-arkay@arkaye.org@imap.1and1.com/Spam.imapmbox/Messages
FILESUFFIX=emlx
START=300570
FINISH=302099
# Note: Missing Mesgs between START and FINISH values; 607 files total/799 spam
OUTFILE1=~/SpamRawData1.txt
OUTFILE2=~/SpamRawData2.txt
OUTFILE2A=~/SortedSpamData2A.txt
OUTFILE2B=~/SpamRawData2B.txt
OUTFILE2C=~/SortedSpamData2C.txt
OUTFILE2E=~/SpamRawData2E.txt
OUTFILE3=~/SpamRawData3.txt
OUTFILE3A=~/SpamRawData3A.txt
OUTFILE3B=~/SortedSpamData3B.txt
OUTFILE3C=~/SortedSpamData3C.txt
OUTFILE4=~/SpamRawData4.txt
OUTFILE4A=~/SortedSpamData4A.txt
OUTFILE5=~/SpamRawData5.txt
OUTFILE5A=~/SpamRawData5A.txt
OUTFILE5B=~/SortedSpamData5B.txt
OUTFILE6=~/SpamRawData6.txt
OUTFILE6A=~/SortedSpamData6A.txt
OUTFILE7=~/SpamRawData7.txt
OUTFILE7A=~/SortedSpamData7A.txt
OUTFILE7B=~/SortedSpamData7B.txt
KEYWORDS=~/Keywordsfile
# Data of interest: Date and Time [1] [Done]
# Target post [2] [Done] See SortedSpamData2.txt for counts
# Author + IP Addresses [3] [Done] See SpamRawData3A.txt for Author only
# whois for IP address (May be forged) [4] [Done]
# Email Address (Especially Email Domain) [5] [Done] also
# SpamRawData5A.txt for email domains only
# URL [6] [Done] Segregate https: and http:
# Key Words or Phrases (i.e. 2 words ending in !) [7] [Done]
#
# Extract Date and Time and store in $OUTFILE1
#
awk '/^Date: /' $DIR/*.$FILESUFFIX | sed -e 's/^Date: //' > $OUTFILE1
#
# Extract Target post (Use html line in body in case of duplicates)
#
awk '/^http:\/\/www.arkaye.com\/blog\/2015/' $DIR/*.$FILESUFFIX | sed -e 's#^http://www.arkaye.com/blog/2015/../##' | sed -e 's#/$##' > $OUTFILE2
cat $OUTFILE2 | sort | uniq -c | sort -rn > $OUTFILE2A
# -------------> below finds line in all messages
awk '/^A new comment on the post /' $DIR/*.$FILESUFFIX | sed -e 's/^A new comment on the post //' | sed -e 's/ is waiting for.*$//' > $OUTFILE2B
awk '/^A new pingback on the post /' $DIR/*.$FILESUFFIX | sed -e 's/^A new pingback on the post //' | sed -e 's/ is waiting for.*$//' >> $OUTFILE2B
awk '/^A new trackback on the post /' $DIR/*.$FILESUFFIX | sed -e 's/^A new trackback on the post //' | sed -e 's/ is waiting for.*$//' >> $OUTFILE2B
cat $OUTFILE2B | sort | uniq -c | sort -rn > $OUTFILE2C
#
# Extract Author Name/Link with IP information (Use Author: line in body)
#
awk '/^Author : /' $DIR/*.$FILESUFFIX | sed -e 's/^Author : //' > $OUTFILE3
awk '/^Author : /' $DIR/*.$FILESUFFIX | sed -e 's/^Author : //' | sed -e 's/(.*$//' > $OUTFILE3A
sort $OUTFILE3A | uniq -c | sort -rn > $OUTFILE3B
cut -d " " -f1 $OUTFILE3A | sort | uniq -c | sort -rn > $OUTFILE3C
#
# Extract IP Address from Whois : line
#
awk '/^Whois : /' $DIR/*.$FILESUFFIX | sed -e 's/^Whois : http:\/\/whois.arin.net\/rest\/ip\///' > $OUTFILE4
sort $OUTFILE4 | uniq -c | sort -rn > $OUTFILE4A
#
# Extract E-mail Address E-mail : line
#
awk '/^E-mail : /' $DIR/*.$FILESUFFIX | sed -e 's/^E-mail : //' > $OUTFILE5
awk '/^E-mail : /' $DIR/*.$FILESUFFIX | sed -e 's/^E-mail : .*@//' > $OUTFILE5A
sort $OUTFILE5A | uniq -c | sort -rn > $OUTFILE5B
#
# Extract URL : line
#
awk '/^URL : /' $DIR/*.$FILESUFFIX | sed -e 's/^URL : //' > $OUTFILE6
sort $OUTFILE6 | uniq -c | sort -rn > $OUTFILE6A
#
# Extract Keywords from Comment text
#
# Consider as key words:
# See KEYWORDS Variable above
for i in $KEYWORDS
do
awk '/^Comment:/,/^Approve it:/' $DIR/*.$FILESUFFIX | grep "$i"
done >> $OUTFILE7
while read i
do
echo $(grep -c "$i" $OUTFILE7) $i
done < $KEYWORDS >> $OUTFILE7A
cat $OUTFILE7A | sort -rn > $OUTFILE7B
# END OF spamscript.bash
The following is a partial sample E-mail notification instance to me that allows the script to work properly:
From: WordPress [Masked]
Subject: [Math-Linux Insights] Please moderate: "Permutations Count On Factorials"
Date: February 22, 2015 6:20:13 PM PST
A new comment on the post "Permutations Count On Factorials" is waiting for your approval
http://www.arkaye.com/blog/2015/02/permutations-count-on-factorials/
Author : Rodent Exterminator St Catherines (IP: 23.106.66.219 , 23.106.66.219.rdns.as15003.net)
E-mail : columbuseagle@gmail.com
URL : https://www.youtube.com/watch?v=KvPxEUBqmLY
Whois : http://whois.arin.net/rest/ip/23.106.66.219
Comment:
You need to take part in a contest for one of the greatest blogs on the web.
I am going to recommend this web site!
The following table shows the number of comment Email sent to the targeted post (with post date) for approval:
| # | Post Title | Post Date |
| 130 | Permutations Count On Factorials | 2-19-2015 |
| 101 | Factorials For Fun | 1-15-2015 |
| 96 | π Places | 1-21-2015 |
| 86 | Sample Page | 1-15-2015 |
| 77 | About Math-Linux Insights | 1-15-2015 |
| 71 | Hello world! | 1-15-2015 |
| 36 | π GPS (Greater Precision Solutions) | 2-4-2015 |
| —– | ||
| 598 |
It was interesting that the commenters’ “programs” failed to distinguish my original content from WordPress generated content (or perhaps it was deliberate). Normally, Moderator rejection is nearly certain if the comment’s context is inappropriate or misdirected.
The most recent post in February had the largest number of Comment E-mails associated during the 6 days it existed and unregistered comments were allowed. Posts with html characters (i.e. of the form: &xxx; ) had unexpectedly fewer comments, especially since the GPS post came after the places post.
[3] WHO: Author
Each Comment has associated with it an Author name. This can be a userid or a link to a web page, video or web page description or gibberish. From the script generated files, I manually summarized and counted a family of descriptors to a single “Author” or keyword name. This was recounted and displayed based on a reverse numerical sort, general keywords that are associated with an Author name two or more times are:
15 best
12 Atlas Chalet
12 travertine tile
10 Bed Bug
9 Manhattan
9 dental
9 roof
8 =D7=A9=D7=99=D7=A8=D7=95=D7=AA=D7=99
8 how to repair
8 personal injury
7 Pest
7 Richmond Virginia (VA) best personal injury
6 cleaning
6 cosmetic
5 commercial
5 cost of
5 criminal
5 hail
5 how much
5 plumber
5 residential
5 tile
4 Insect
4 abogados de accidente Miami
4 brooklyn
4 dentist
4 find
4 hvac
4 title loans
3 Ant
3 Carpenter Ant
3 Exterminator
3 Home
3 Rat
3 Wildlife
3 affordable
3 cash
3 dui
3 estimated
3 get
3 marble
3 paid
3 payday
3 replacing
3 sealing
3 teeth
2 24 hr emergency
2 Ants
2 Atlas Chalet Warranty Cobb
2 Brittany
2 Click [Hh]ere
2 Defective Atlas Chalet Shingles
2 Home Pest Control Service
2 Residential Pest Control
2 Richmond
2 Roach
2 Rodent
2 Roof
2 SEO
2 TX
2 air conditioner
2 appliance repair
2 atlanta
2 best music
2 best paid survey sites
2 best personal injury attorney Richmond Virginia
2 blitz brigade hack
2 cat toys
2 cheap
2 commercial appliance repair
2 cost to
2 credit repair
2 deer hunter 2014
2 family law
2 free
2 garage door
2 go
2 google
2 great site
2 herpes cure
2 how to find a
2 it
2 jetpack joyride
2 knights and dragons
2 lawyer
2 miami
2 nyc
2 paid survey sites
2 plumbing
2 pou
2 pozyczka
2 queens
2 redolex.com
2 replacement gas furnace
2 reviews
2 seo
2 seo plugin
2 shingles repair
2 solar panel
2 solar power
2 storm
2 surveys for money
2 teeter hang ups review
2 title
2 try this site
2 tucson dui help
2 zesp=C3=B3=C5=82 na wesele Krak=C3=B3w
[4] WHERE: Country, State, City
WordPress associates an IP (v4) address (e.g. of the form nnn.nnn.nnn.nnn, where each nnn ranges independently between 0 and 255) with every comment. This allows me to pinpoint how many times the same IP address is used to issue a comment. Also, there is a website, What Is My IP? that lets you enter an IP address and it returns, among other things, the Latitude, Longitude, City, State and Country and a map segment associated with that IP address location.
In a file, I extracted the counts of IP addresses associated with the comments and then manually augmented that file with the Country, State and City. The highest repeated IP address (108.177.146.70) was 24, from Phoenix, Arizona. I then added up all the counts from each of the same cities and produced the following table (minus the IP addresses):
465 Arizona Phoenix
22 New York Buffalo
15 France Paris
12 Sweden Stockholm
7 Germany Frankfort
5 Nevada Henderson
5 California Los Angeles
5 United Kingdom London
4 Texas Dallas
3 Indiana Zionsville
3 Canada Quebec Montreal
3 China Caizi Zhen
3 Delaware Dover
3 New York New York City
3 Netherlands Dronten
3 Romania Media
3 Netherlands Amsterdam
2 Colorado Fort Collins
2 Alabama Montgomery
2 Florida Miami
2 Russia Moscow
2 Switzerland Zurich
2 Romania Moldova
2 California Fresno
1 Lebanon Beirut
1 China Sichuan Mianzhu
1 Taiwan Taipei
1 China Shaanxi Xian
1 Poland Warsaw
1 Germany Berlin
1 Illinois Chicago
1 Illinois Lombard
1 Maryland Baltimore
1 Russia Dubna
1 Washington Spokane
1 Russia Saint Petersburg
1 Germany Munich
1 North Carolina Greensboro
1 Ukraine Uzhgorod
1 Poland Gdansk
1 Romania Lasl
1 Russia Murmansk Kovdor
1 Iowa Cloud
Therefore `bb (465/597)` or nearly 78% of the |s,p.a,m| comes from 44 servers (with unique IP addresses) in Phoenix, Arizona. These 44 unique servers are counted using:
cat SortedSpamData4C.txt | grep –c ‘Arizona Phoenix’
[5] REPLY: Email Address
Turning now to the Email addresses associated with the 597 comment Emails, there were 49 unique email addresses used. gmail.com had the preponderance of Email domains with 185; The primary domains .de (Germany) had 8 and .net had 11.
185 gmail.com
34 arcor.de
28 yahoo.com
27 zoho.com
26 freenet.de
25 gawab.com
24 googlemail.com
23 web.de
23 inbox.com
22 bigstring.com
21 yahoo.de
21 t-online.de
21 aol.com
15 gmx.de
13 hotmail.com
12 gmx.net
9 live.com
7 live.de
6 hotmail.de
6 care2.com
4 wildmail.com
4 snail-mail.net
4 peacemail.com
3 animail.net
2 yepmail.net
2 vegemail.com
2 msn.com
2 moose-mail.com
2 mailservice.ms
2 mailsent.net
2 mail.com
2 justemail.net
2 imap.cc
1 xvrqyw.com
1 whale-mail.com
1 swift-mail.com
1 ssl-mail.com
1 speedpost.net
1 ownmail.net
1 mailworks.org
1 mailup.net
1 mailnew.com
1 mailmight.com
1 mailc.net
1 mailas.com
1 fastmessaging.com
1 fastmail.net
1 fastem.com
1 fast-mail.org
[6] WHY: Click On URL
Next, we consider the URLs associated with the Comments. In addition to the 597 comments were 6 trackbacks (generated by others) and 2 pingbacks (generated by me).
Protocols used: https = 375 http = 230 Total = 605
Specific Selected URL Domains (enclosed with /s):
# URL
366 www.youtube.com
69 youtu.be
24 www.facebook.com
17 .*.[Gg]oogle.com
7 redolex.com
4 www.yelp.ca
4 bitly.com
3 scapca1.net
2 www.pinterest.com
1 twitter.com
Keyword URL Domains (No right / )
# URL pattern
16 .*survey.*
8 .*porn.*
As can be seen, youtube and its variant represented 435 URLs that commenters used to represent themselves for viewing purposes.
[7] WHAT: Message Keywords
The following table shows the keywords I determined to be peculiar to |S,p.a,m| comments and their popularity, in descending order. Based on the script output file, the following keywords were manually summarized and commandline counted.
# Keyword
294 nice
271 won
228 ans
199 info
137 pleasant
114 off topic
80 fastidious
47 brussels
45 heads up
42 creative writing
39 useful information
38 convey
28 comeback
27 masterpiece
25 pals
24 subject matter
24 donate
23 whilst
22 you relied on the video
22 go after your heart
21 hyperlink
20 at the glance out
19 peer
19 onderful site
14 loading velocity
14 arena
13 such a lot
11 uncanny
9 vefy
9 bravery
8 must read
7 I say to you
6 un-ambiguity
6 take a signal
6 preserveness
6 energetic article
6 I have a mission
4 precious knowledge
1 what a information
1 unpredicted
1 killing my time
1 did not happened
1 Grrrr…
So there it is. Probably much more than you wanted to know about how comment
|S,p.a,m| can find you as a result of normal blog post publicity on WordPress’ part.
Perhaps this data can offer insights to others plagued with similar experiences.
We may have to go back to the old tradition, as when researchers wrote papers in the last century. They invited you to read their paper (and offer improvements). Nothing went viral for years, if ever.
The Internet’s ability as a conduit and enabler for many “agents” to visit sites, leave (non)messages or even crash websites through directed, overwhelming traffic are instances of unwanted popularity. It is analogous to Standup Comedians being heckled or Government Spokespeople/Invited Speakers being vocally protested or the Signal being accompanied by a significant amount of Noise.
The most elegant solution to this, to my mind, lies in creating a virtual lightning rod decoy to attract the unwanted (Linux has a facility called /dev/null .), while creating and sheltering a direct conduit for those who wish to offer dialogue via cogent questions, differing opinions or other helpful reactions.