π (say ‘pie’) is the lower case Greek letter symbol that stands for a number defined as the ratio of the circumference (C) of a circle divided by its diameter (d).
Circumference means the distance around something, like a circle or a polygon. A synonym would be perimeter.
A diameter is the length of a line that is drawn starting from any point on the circle’s boundary and going through the center point of the circle and then continuing to the opposite boundary point. A radius (r) is the length of a line drawn from the center to any point on the circle’s boundary. It is half the diameter. It’s clearer in the diagram:
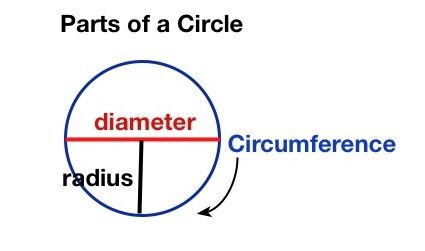
As a formula (no numbers, please), we write:
`pi = C/d ` [1]
If d = 1 inch, then because π has a fixed, constant value, C must be equal to that value of π inches.
A closely related formula involving π involves the Area A, of a Circle and its radius r, (remember? – half of the diameter’s length). The formula is:
`pi = A/r^2 ` [2]
Most descriptions of π state when it was first historically used and trace a series of numerical refinements in its approximated value over the last 4500 years.
A chronology of the computation of π from 2500 BC (calculated as `22/7` ) to the present is shown in the following link: π Chronology
It shows the date, the person, milestone or event and the decimal value of π (or the correct number of decimal digits after 3.) up through October 8, 2014, when π had been computed and verified (anonymously) to `1.33∙10^13` (over 13 Trillion) decimal digits.
Classifications
It turns out that π is an irrational number. (Johann Heinrich Lambert proved this in 1761.)
This means that we cannot discover a fraction that provides its value exactly. Writing its decimal digits never ends. So over the years, mathematicians have labored to compute π accurately to more and more decimal places using “good” fractions and infinite series where only the first “few” terms are evaluated and summed.
It is also true the π is a transcendental number. A transcendental number is an irrational number that is not an algebraic number. An algebraic number is one that satisfies a polynomial equation with a finite number of terms and with rational coefficients. So, for example, `sqrt(2)` is an irrational (non-repeating decimal number) and an algebraic number, since it is a solution to the algebraic equation: `x^2 = 2`
For non-algebraic equations, we have two equations from trigonometry, which use `pi/4` radians rather than 45 degrees:
tangent`(pi/4) = 1` [3]
and particularly its counterpart:
arctangent`(1) = pi/4` [4]
is used as a starting point for determining π more precisely.
Rational (Fractional) Approximations
Methods of approximation started with Archimedes, who, around 250 BC, applied the method of exhaustion with inscribed and circumscribed regular polygons to enclose the lower and upper bounds of area and circumference of the circle. Shown below are inscribed and circumscribed pentagons, hexagons and octagons (n = 5, 6, 8). Starting with a hexagon, he doubled the sides for inner and outer n-gons until n = 96, finding the inner and outer perimeters at each value of n.
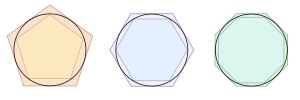
Archimedes found bounds for π as:
`3 + 10/71 < pi < 3 + 10/70` or `223/71 < pi < 22/7` [5]
This gives the value of π to 2 decimal places, as 3.14.
A Cool Procedure And Shell Script For a better Fraction for π
Using the circumference formula [1], we can create a procedure based on one suggested by Rhett Allain (See:
Best Fraction For π to calculate a fraction that represents π for a given number of digits.
For reference, suppose πref is set to 3.14159265358979, which is to 14 decimal places. We use this 12 step procedure:
- Set πref = 3.14159265358979
- Set (1/πref) = 0.31830988618379
- Set loopcount = 500
- Set C = 22
- Set D = 7
- Set Percentage Error = 0.001
- Is loopcount = 0 ?
Then output BestC, BestD, BestC/BestD, Error, BestLoop
and stop - Set πest = C/D
- Calculate Absolute Value of E = | (πref – πest) / πref |
via E = | (πref – πest) ∙ (1/πref) | - Is E < Error ?
Then set BestC = C, set BestD=D, set Error = E,
and set Bestloop = 500 – loopcount - Is πest < πref ?
Then add 1 to C and go to step 12
Otherwise add 1 to D and go to step 12 - Subtract 1 from loopcount and go back to step 7 and compute new πest
Here is the bash shell script that I wrote to program this algorithm. It takes slightly under 7.5 seconds (what’s your hurry?) to finish 500 iterations (on a 2010 vintage 32-bit MacBook Pro) and 3.55 seconds on a 64-bit GNU/Linux Server.
The script successfully finds the fraction
`355/113` = 3.141592920353982 [6]
a close approximation to the reference π that is accurate to 6 decimal places. The percentage error using this fraction is 0.0000084913679%
In this script, the Linux utility bc is needed to offer/preserve 15 decimal place precision in the computations it performs. The shell facilities for operating with numbers using anything other than positive integers are minimal.
#! /bin/bash
USAGE="Usage: pifraction.bash"
# Version 1.0 by arkay on 1/17/2015
# Version 1.1 by arkay on 1/18/2015
# Computed (1/Pi_ref) once and used it to multiply for
# % difference.
# Set Starting values for variables
Pi_ref="3.14159265358979"
Pi_ref_inv="0.31830988618379"
loopcount=500
C=22
D=7
Error="0.001"
# loop 500 times
until (( loopcount < 1 ))
do
# Calculate Pi.est
Pi_est=$(echo "scale=15; $C/$D" | bc -l)
# Calculate the percentage error E
E=$(echo "scale=15; ($Pi_ref - $Pi_est)*$Pi_ref_inv" | bc -l)
if [ "${E%%[0-9.]*}" == "-" ] #Apply Absolute Value:
# extract first character of E, either "–" or ""
then
E=$(echo "scale=15; (-1)*$E" | bc -l)
fi
# Compare E with current minimum % Error
T=$( echo "scale=15; $E<$Error" | bc -l )
if [ "$T" -eq "1" ] # bc returns 1 if inequality true
then
BestC=$C; BestD=$D; Error=$E;
BestLoop=$(expr 500 - $loopcount)
fi
# Compare Pi_est with Pi_ref
S=$( echo "scale=15; $Pi_est<$Pi_ref" | bc -l )
if [ "$S" -eq "1" ] # bc returns 1 if inequality true
then
(( C += 1))
else
(( D += 1))
fi
(( loopcount -= 1 ))
done
# Produce the results
BestCoverD=$(echo "scale=15; $BestC/$BestD" | bc -l)
echo "BestC=$BestC BestD=$BestD BestCoverD=$BestCoverD"
echo "Pi_ref=$Pi_ref Error=$Error BestLoop=$BestLoop"
exit # Normal stopping point
# End of pifraction.bash
Output results from this shell script are shown as:
BestC=355 BestD=113 BestCoverD=3.141592920353982
Pi_ref=3.14159265358979 Error=.000000084913679 BestLoop=439
In my next post about π, I will write about greater decimal place approximators and Interesting π activities to try.
Oh, one last thing…
This is a delightful Math Trick attributed to Martin Gardner:
Write all 26 letters of the alphabet, but start with the letter J as shown:
JKLMNOPQRSTUVWXYZABCDEFGHI
Then, remove all the letters that have vertical symmetry as shown:
JKL N PQRS Z BCDEFG
Now, count the letters that remain in each subset: 3 1 4 1 6.

I didn’t understand the math trick. What do you mean by “vertical symmetry?”
Hi Barb,
To explain this, write the letter Y. If you now place a real (or imaginary) mirror that stands out from the page on top of the letter Y at its center, then by looking at the mirror side and the right half of the letter, The letter Y can still be seen. Whenever this is true, the letter has vertical symmetry.
If you notice the letters that are removed from the alphabet starting with J, each has a vertical symmetry. I hope this helps you to understand vertical symmetry and the math trick.
Pingback: π GPS (Greater Precision Solutions) | Math-Linux Insights