In my previous blog post, Factorials For Fun, I wrote about factorial notation and its amenability to being calculated by iteration and recursion.
In this post, I want to relate the use of factorials in permutations, named by John H Conway as arrangement numbers. While there is a factorial-based formula for counting how many permutations, it takes much more discipline to enumerate them all correctly (boring too, if done by hand). This has become such an extensive review, so I will relate in a separate future post factorials with combinations (choice numbers, also named by John H. Conway).
A Fundamental Counting Principle
The Product Rule:
Suppose that a procedure can be split into a sequence of k tasks. If there are n1 ways to do the first task and for each of these n1 ways, there are n2 ways of doing the second task, and generally, for all of these n1, n2, …, nk-1 ways, there are nk ways of doing the kth task, then there are
`bb n_1*n_2*…*n_k`
ways to do the entire procedure.
This principle is applied whenever you are choosing each object from its own group.
Suppose your camping wardrobe is made up of 2 pairs of hiking boots, 3 vests, 6 shirts, 1 hat and 3 jackets. How many different outfits are possible?
Since each item belongs to its own group, we have: `bb 2*3*6*1*3 = 108` different outfits.
Permutations
A permutation of n objects is an ordered arrangement of n distinct items (objects) in a row.
Consider 3 coins, such as a Nickel, Dime, and Quarter. The Nickel (N), Dime (D) and Quarter (Q), in that order, is a single permutation of the three coins. The entire list of all possible permutations of the three coins is here:
{N, D, Q}, {N, Q, D}, {Q, N, D}, {D, N, Q}, {D, Q, N}, {Q, D, N} [1]
This list of permutations has a count of 6. This is equivalent to 3⋅2⋅1 arrangements.
This is because the first coin can be any one of 3 denominations (3 ways). Once chosen, the second coin can be any one of the remaining 2 denominations (2 ways). So for the first two positions, there are 3⋅2 ways. Once the second coin is chosen, the third coin is whatever denomination remains and is chosen (1 way). So for the first three positions, there are 3⋅2⋅1 ways.
Because each position is filled from what is sequentially available (remaining) among the 3 coins, this is called selection without replacement.
Question: How many permutations (arrangements) of n distinct objects are possible (without replacement)?
Value of k: 1 2 3 k (n-1) n
Ways to choose k: n (n-1) (n-2) . . . (n – k + 1) . . . 2 1 [Table 1]
Row position: — ——- —— ————- — —
In the first position, we can choose any of the n objects. Choose one.
In the second position, since one object was already chosen, we can choose any of the
(n-1) objects. Choose one.
In the third position, since two objects have already been chosen, we can choose any of the
(n-2) objects. Choose one.
In this same way, in the kth position, we can choose (n – k + 1) objects since k objects have already been selected. Choose one.
Finally, for the last position, since all but one, namely (n-1) objects have been chosen, there is only 1 object left to choose and put in the last position. Choose it and complete a single arrangement (ordering) in a row.
Therefore the number of ways to choose (arrange) n objects out of a total of n objects is:
n⋅(n-1)⋅(n-2)⋅…⋅2⋅1 = n! [2]
And the number of ways (permutations) to choose k (unique) objects out of a total of n (unique) objects is:
n⋅(n-1)⋅(n-2)⋅…⋅(n-k+1) = `bb (n!)/((n-k)!)` = `bb _nP_k` [3]
The fraction in the center in [3], is the product of all the numbers from 1 to n, (i.e. n!) except for those being a product from 1 to n – k ( which is (n – k)! ).
Because n! is a multiple of (n – k)! , this artificial fraction evaluates to a product of consecutive integers, below, the arrangement numbers:
n⋅(n-1)⋅(n-2)⋅…⋅(n-k+1)
This “fraction” in [3] has a variety of notational labels and all mean the same thing:
Symbols Spoken or Meaning When k = n
P(n,k) a k-permutation P(n,n) = n!/0! = n!
pnk a k-permutation arranged in a row pnn = n!/0! = n!
nPk the permutations of n things taken k at a time nPn = n!/0! = n!
(n)k a k-list (n)n = n!/0! = n!
nk n to the k falling (falling power) nn = n!/0! = n!
n factorial is also recursively written as:
n! = n⋅(n-1)! [4]
which is valid for all positive integers n ≥ 1.
It is also true that, by solving [4] for (n-1)! , we have:
(n – 1)! = `bb (n!)/n`
(n – 1)! also represents the number of circular arrangements (or necklaces) of n distinct objects. This is because two permutations (i.e. complete placements of people around a circular table) can be considered identical if one becomes the other by rotating the circle (or table).
There are n ways to rotate the circle (or table). So n divides the n!
In summary, n! is the count of the number of permutations (or linear arrangements) of n distinct objects in a row and (n-1)! is the count of the number of circular permutations (or arrangements).
Computation Aids: Online Calculators
The website calculatorsoup.com has these special permutation calculators available for those dealing with larger values of n. They are:
This calculator has examples to show how to use and Calculate nPk where 0 ≤ n, k ≤ 9999. See:
Permutations Calculator.
and
Circular Permutations Calculator: Calculates (n-1)! where 0 ≤ n ≤ 9999. See:
Circular Permutations Calculator
Other specialized calculators are interspersed further below.
5 Examples
(1) How many different ways can the letters in the word numerals be arranged?
Since different ways is a synonym for arrangements, and the 8 letters are distinct, the permutation formula [2] (or [3] with k=n] , expressed as n! , is to be applied:
8! = 8⋅7⋅6⋅5⋅4⋅3⋅2⋅1 = 40320 ways
(2) How many ways are there to select a first-prize winner, a second-prize winner and a third-prize winner from 50 different people who have entered a contest?
In this question, it is important to know which person wins which prize. So the number of ways to choose the three prize-winners is the number of ordered selections of 3 people (out of 50).
So we consider that the first prize can be won by any of the 50 people; then the second prize can be won by any of the remaining 49 people; and the third prize can be won by any of the remaining 48 people. This is reflected in formula [3], where n = 50 and k = 3.
50P3 = `bb (50!)/((50-3)!) = ( 50*49*48*…*1)/(47*46*45*…*1)` = 50⋅49⋅48 = 142100 ways.
(3) How many permutations of the letters STUVWXYZ contain the consecutive lettered string XYZ ?
Because the consecutive lettered (sub)string XYZ must all appear as an ordered group (first X, then Y, then Z) in the larger 8 lettered arrangement, we can think of the string XYZ as a single entity.
Then the number of arrangements of {S, T, U, V, W, XYZ} is based on 6 items rather than 8. So:
6! = 6⋅5⋅4⋅3⋅2⋅1 = 720 ways
(4) In how many ways can 9 people be seated around a circular table?
Because this fits the conditions for a circular permutation (with arrangements that can be rotated being considered indistinguishable), we use the formula in [5] with n = 9:
(9 – 1)! = 8! = 8⋅7⋅6⋅5⋅4⋅3⋅2⋅1 = 40320 ways.
(5) Find the number of ways in which 5 people Al, Betty, Cam, Dana and Ed have place settings (seats) at a circular table, such that:
(i) Dana and Ed must always sit together, and
(ii) Al and Betty must not sit together.
Because this fits the conditions for a circular permutation (with rotations of any arrangement being considered equivalent), we will start with formula [5].
Consider the first restriction. Dana and Ed sitting together represent a couple, a single entity. So n = 4 {Al, Betty, Cam, Couple} or {a, b, c, de) and:
2⋅(4 – 1)! = 2⋅3! = 2⋅3⋅2⋅1 = 2⋅6 = 12
In the expression evaluation, as there are two positions the couple can assume, the 6 is multiplied by 2 to get 12.
To show each circular arrangement, I visualized a clock with de at the Noon position, a at the 3:00, b at the 6:00 and c at the 9:00 position, respectively. By keeping de anchored at the Noon position, the rest of the people (n – 1) can be permuted (arranged) normally for counting purposes and rotations do not occur.
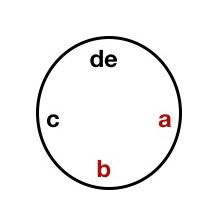
Using initials, the Part (i) count of 12 arrangements enumerates as follows:
(abcde), (acbde), (cabde), (cbade), (bacde), (bcade),
(abced), (acbed), (cabed), (cbaed), (baced), (bcaed)
Now consider the second restriction: Al and Betty must not be neighbors.
This means that Al and Betty (a and b) must be separated on either side of a or b by both c and de. Notice that the four uncolorful arrangements are just the ones that are needed.
We can determine this more analytically by thinking about creating four quartets: adeb, bdea, aedb, beda, which separate a and b and which get permuted with c in only 1 way each (this is because cadeb and adebc are equivalent rotations). Since c must be on the outside of the quartet, c is also between b and a (or a and b).
Alternatively, we can delete from the part (i) enumeration of 12, the 8 arrangements where a and b are next to each other. So we must subtract from the list of 12, these 8 arrangements: (abcde), (cabde), (cbade), (bacde), (abced), (cabed), (cbaed) and (baced).
This leaves 4 circular arrangements (acbde), (bcade), (acbed) and (bcaed) that simultaneously fulfill the two restrictions.
Permutation Relaxations
So far, this discussion focused on Permutations that were distinct and had no repetitions and were counted without replacement. How does the counting change if we allow repetitions or if we allow replacement or both?
- Permutations with repetitions
The rule is that if there are zero or more repetitions of an object, because they are indistinguishable objects, their multiplicity factorial must divide the overall arrangement factorial to get the proper count. (with zero repetitions, we have a multiplicity of 1; i.e. the object is unique.)`bb (n!)/(a!*b!*c!*…*k!)` , where a+b+c+…+k = n [6]
As an example, suppose we want to know how many different ways the distinct letters in the word bananas can be arranged? We calculate:
`bb (7!)/(3!*2!) = (7*6*5*4*3*2*1)/((3⋅2⋅1)⋅(2⋅1)) = 7*6*5*2` = 420 .
This is because ‘a‘ is repeated three times and ‘n‘ is repeated twice; for each of these letters, the repetitions are indistinguishable, so each multiplicity factorial (3! and 2!) must divide the factorial of the 7 letter word to get the correct count.
- Permutations with replacement
If we are counting Permutations with replacement, then Table 1 changes and becomes:Value of k: 1 2 3 k (n-1) n
Ways to choose k: n n n . . . n . . . n n [Table 2]
Row position: —- —- —- —- —- —-In the first position, we can choose any of the n objects. Choose one.
In the second position, we can choose any of the n objects. Choose one.
In the third position, we can choose any of the n objects. Choose one.In this same way, in the kth position, we can choose any of the n objects. Choose one.
Finally, for the last position, we can choose any of the n objects. Choose one.
In this way, we complete a single arrangement (ordering) in a row.
Therefore the number of ways to choose (arrange) n objects out of a total of n
objects (with replacement) is:n of these
` <———>`
n⋅n⋅n⋅…⋅n⋅n = nn [7]And the number of ways (permutations) to choose k (unique) objects out of a total of n (unique) objects (with replacement) is:
k of these
` <———>`
n⋅n⋅n⋅…⋅n⋅n = nk [8]There is a Permutations With Replacement Calculator. It offers examples of how to use and Calculate nr where 0 ≤ n, r ≤ 9999. See:
Permutations With Replacement CalculatorAn Example:
U.S. zip (postal) codes consist of an ordering of five digits, hyphen, followed by four digits chosen from 0-9 with replacement (i.e. digits may be reused). How many zip codes are in the set of all possible zip codes?
Since we are looking for arrangements with replacement, we use n, the number of digits to be 0-9, which is 10 digits and the number of positions of the zip code, which is 9.
Using the formula [8], we calculate:
109 = 1 Billion.
Since the zip code 00000-0000 is not used, we subtract it from 1 Billion to get:
999,999,999 different zip codes.
If 00000-nnnn are also to be unused, we have instead:
109 – 104 = 9.9999 × 108 = 999,990,000 different zip codes.
- Derangements (and subfactorials)
A Derangement is a permutation of the elements of n objects or elements, such that no element appears in its original position. If an original permutation is {1, 2, 3, 4, 5}, one derangement would be {2, 3, 4, 5, 1}.The symbol !n (sometimes called a subfactorial), represents the number of derangements of n objects and its formula is:!n = n!`bb sum_(k=0)^n ((-1)^k)/(k!)` [9]
In this formula, n ≥ 2. Here are the listings of !n up to n=4.
!0 = 1 (the empty permutation)
!1 = None
!2 = 1 (21)
!3 = 2 (231) (312)
!4 = 9 (2143), (2341), (2413), (3142), (3412), (3421), (4123), (4312), (4321)Derangements with a single fixed point are another special permutation calculation. The number of permutations having at least one fixed point, (e.g.: {2, 4, 3, 5, 1} thus not being (a complete) derangement, is given by:
n! – !n = n! – n!`bb sum_(k=0)^k ((-1)^n)/(k!) = n!sum_(k=1)^n ((-1)^k)/(k!)` [10]
Another Example:
You have 6 balls in 6 different colors, and for every ball you have a box of the same color. How many derangements do you have, if no ball is in a box of the same color? If at least one ball is in a box of the same color?
To apply [9] to this problem, we calculate:
!6 = 6!`bb ((1 – 1 + 1/2 – 1/6 + 1/24 – 1/120 + 1/720)) =`
6*5*4*3 – 5! + 6*5 – 6 + 1 =
360 – 120 + 30 – 6 + 1 = 265For the second part of the question, keeping in mind that what is not a derangement is a “partial” derangement, we subtract the total number of derangements from the total number of permutations.
6! – !6 = 720 – 265 = 455
or evaluating the right side of [10] explicitly, we have
6!`bb ((1 – 1/2 + 1/6 – 1/24 + 1/120 – 1/720)) =`
720 – 6*5*4*3 + 5! – 6*5 + 6 – 1 =
720 – 360 + 120 – 30 + 6 – 1 = 455 - Permutation Cycles
A permutation cycle is a subset of a permutation whose elements trade places with one another.
For example, in the permutation group {4, 2, 1, 3}, (143) is a 3-cycle and (2) is a 1-cycle. Here, the notation (143) means that starting from the original ordering
{1, 2, 3, 4}, the first element is replaced by the fourth, the fourth by the third, and the third by the first, i.e., `bb 1 rarr 4 rarr 3 rarr 1`.( `1, 2, 3, 4` ) So `1 rarr 4 , 4 rarr 3, 3 rarr 1` creates the 3-cycle (143) and
`darr darr darr darr` `2 rarr 2` creates the fixed point or 1-cycle (2).
( `4, 2, 1, 3` ) So we have, (143)(2) making up the two cycles in the
permutation group {4, 2, 1, 3}.( See: Weisstein, Eric W. “Permutation Cycle.” From MathWorld–A Wolfram Web Resource. <mathworld.wolfram.com/PermutationCycle.html> )
- Odd And Even Permutations
So is {4, 2, 1, 3} an odd or even permutation?
By definition, an odd permutation is a permutation obtainable from an odd number of two-element swaps, i.e., a permutation with permutation symbol (Levi-Civita signature symbol) equal to -1.
For the initial set (1,2,3,4) the twelve odd permutations are those with one swap (1,2,4,3, 1,3,2,4, 1,4,3,2, 2,1,3,4, 3,2,1,4, 4,2,3,1) and those with three swaps (2,3,4,1, 2,4,1,3, 3,1,4,2, 3,4,2,1, 4,1,2,3, 4,3,1,2).
For a set of n elements and n ≥ 2, there are `bb (n!)/2` odd permutations *, which is the same as the number of even permutations. For n =1, 2, …, the total odd permutations are given by 0, 1, 3, 12, 60, 360, 2520, 20160, 181440, … (OEIS A001710).
(* D’Angelo, J. P. and West, D. B. Mathematical Thinking: Problem-Solving and Proofs, 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 2000. (p.111) and
Weisstein, Eric W. “Odd Permutation” From MathWorld–A Wolfram Web Resource. <mathworld.wolfram.com/OddPermutation.html> )By definition, an even permutation is a permutation obtainable from an even number of two-element swaps, i.e., a permutation with permutation symbol (Levi-Civita signature symbol) equal to +1.
Similarly.
For the same initial (1,2,3,4), the twelve even permutations are those with zero swaps: (1,2,3,4); and those with two swaps: (1,3,4,2, 1,4,2,3, 2,1,4,3, 2,3,1,4, 2,4,3,1, 3,1,2,4, 3,2,4,1, 3,4,1,2, 4,1,3,2, 4,2,1,3, 4,3,2,1).
For a set of n elements and n ≥ 2, there are `bb (n!)/2` even permutations, which is the same as the number of odd permutations. For n=1, 2, …, the numbers are given by 0, 1, 3, 12, 60, 360, 2520, 20160, 181440, … as above. (OEIS A001710).
( See: Weisstein, Eric W. “Even Permutation” From MathWorld–A Wolfram Web Resource. <mathworld.wolfram.com/EvenPermutation.html> )An Odd Permutations Calculator may be used to Calculate `bb (n!)/2` where 2 ≤ n ≤ 100. See:
Odd Permutations CalculatorAlso, An Even Permutations Calculator may be used to Calculate `bb (n!)/2` where 2 < n ≤ 9999. See:
Even Permutations CalculatorSo {4, 2, 1, 3} is an even permutation and its 3-cycle (143) and 1-cycle (2) represent two even cycles.
A rule of thumb is that the if a permutation cycle has an odd number of elements within, it is considered even, otherwise if an even number of elements within, it is considered odd.An analogy exists with odd and even numbers which is also true of permutation cycles:
If two even numbers (cycles) are added together, the result is even.
If two odd numbers (cycles) are added together, the result is also even.
If one even and one odd number (cycles) are added together, the result is odd.
Thus {4, 2, 1, 3} is an even permutation based on two even cycles (143) and (2).
Finally, the rosettacode.org site offers over 70 different computer language codes and scripts (although not any of the Unix/Linux Shells as yet). These programs deal with permutations with or without replacement (as well as that for combinations). See Enumerating Permutations Programs.
The site also has programmatic algorithms for
• permutations with repetitions,
• Finding the missing permutation: finding the missing enumerated permutation from the full set of permutations (47 programs and an interesting discussion tab) See: Find_the_missing_permutation and
• permutations and derangements: See: Derangement programs (26 programs)
I should mention that the most popular applications for permutations are for people that love Scrabble (at least two or more play), Anagrams and Jumble word and cartoon puzzles. Other applications are when a host is planning a formal a sit down, catered meal for at least 6 people that has seating preferences and constraints. As always, if you are unable to successfully seat everyone agreeably, make the problem bigger and invite more guests.
Book References:
Conway, John H., Guy, Richard K., (1995). The Book of Numbers. Springer-Verlag, New York, NY. (p. 66-67)
Knuth, Donald E. (1997). Art of Computer Programming, Volume 1: Fundamental Algorithms, 3rd Ed. Addison-Wesley, Boston. MA.(p. 45-50, 164-167)
Rosen, Kenneth H., Editor-In-Chief (2000). Handbook of Discrete and Combinatorial Mathematics. CRC Press, Boca Raton, FL (p. 84-91, 96-107)
Rosen, Kenneth H. (2012). Discrete Mathematics and its Applications, 7th Ed. McGraw-Hill, New York, NY (p. 385-443)
